Google encontra novas soluções para um dos problemas do milênio usando IA

Em 2000, o Clay Mathematics Institute definiu sete problemas como sendo os maiores problemas dentro da Matemática. Cada um dos sete problemas foram escolhidos por representarem desafios que há décadas ou séculos não foram encontradas soluções. Os problemas estão em diferentes áreas da Matemática, desde geometria até equações diferenciais. Resolver qualquer um desses problemas tem um prêmio de 1 milhão de dólares.

Entre esses problemas, existe o problema de existência e suavidade das equações de Navier-Stokes. Essas equações descrevem o comportamento e a dinâmica de fluidos como água, ar e plasma sendo importante para Meteorologia, Astrofísica e até Física Nuclear. Embora sejam usadas constantemente, ainda não há uma prova matemática rigorosa de que essas equações sempre possuem soluções bem definidas e sem singularidades. Por causa disso, a Navier-Stokes entra com um dos problemas do milênio.

Compreender completamente as equações de Navier-Stokes pode mudar a forma como entendemos turbulência, clima, dinâmica dos oceanos e até processos astrofísicos. Recentemente, o Google anunciou um novo método baseado em Physics-Informed Neural Networks (PINNs) para encontrar soluções para as equações de Navier-Stokes. Segundo a empresa, eles conseguiram soluções inéditas para o problema de Navier-Stokes usando técnicas de inteligência artificial.

Navier-Stokes

Quando se fala de equação de Navier-Stokes, na verdade se refere a um conjunto de equações diferenciais parciais. Essas equações são responsáveis por descrever a dinâmica de fluidos que inclui líquidos, gases e plasmas. O conjunto de equações vem da conservação de massa, momento e energia considerando efeitos como viscosidade, pressão e forças externas.

Apesar de ser usada em quase todas áreas, as equações são complexas de resolver, principalmente em regimes turbulentos. A turbulência é um dos grandes mistérios da Física e da Matemática porque ainda não é bem descrita. Ela gera comportamentos caóticos e estruturas em múltiplas escalas e é impossível obter soluções exatas em muitos casos. Por isso, na prática, recorrem-se a simulações computacionais e métodos numéricos para resolver alguns problemas que envolvam Navier-Stokes.

Ensinando Física para IA

Essa semana, o Google anunciou um novo artigo onde argumentam que encontraram soluções inéditas para as equações de Navier-Stokes. No artigo, os autores descrevem que usaram PINNs para aprender e simular diferentes sistemas de fluidos. As PINNs funcionam para respeitar as equações que descrevem as leis da física daquele sistema. A cada passo, a saída da rede é comparada com o que as equações físicas preveem e o modelo aprende a minimizar o erro.

Ao usar as PINNs dentro da arquitetura do aprendizado, os pesquisadores conseguiram colocar insights matemáticos diretamente no processo de treinamento. Com isso, foi possível encontrar soluções instáveis e evasivas, como singularidades, que não é possível dentro de métodos convencionais. Além disso, os autores conseguiram criar uma estrutura que permite que o modelo aprenda próximo ao limite da precisão computacional.

Encontrando soluções com IA

As descobertas que os pesquisadores do Google encontraram com esse novo artigo envolvem diferentes equações de fluidos. Eles encontraram famílias de singularidades instáveis que nunca foram encontradas antes. Alguns insights foram encontrados como, por exemplo, o parâmetro chamado lambda que representa a velocidade da explosão pode estar relacionado à ordem de instabilidade. Esse padrão foi identificado em duas equações estudadas.

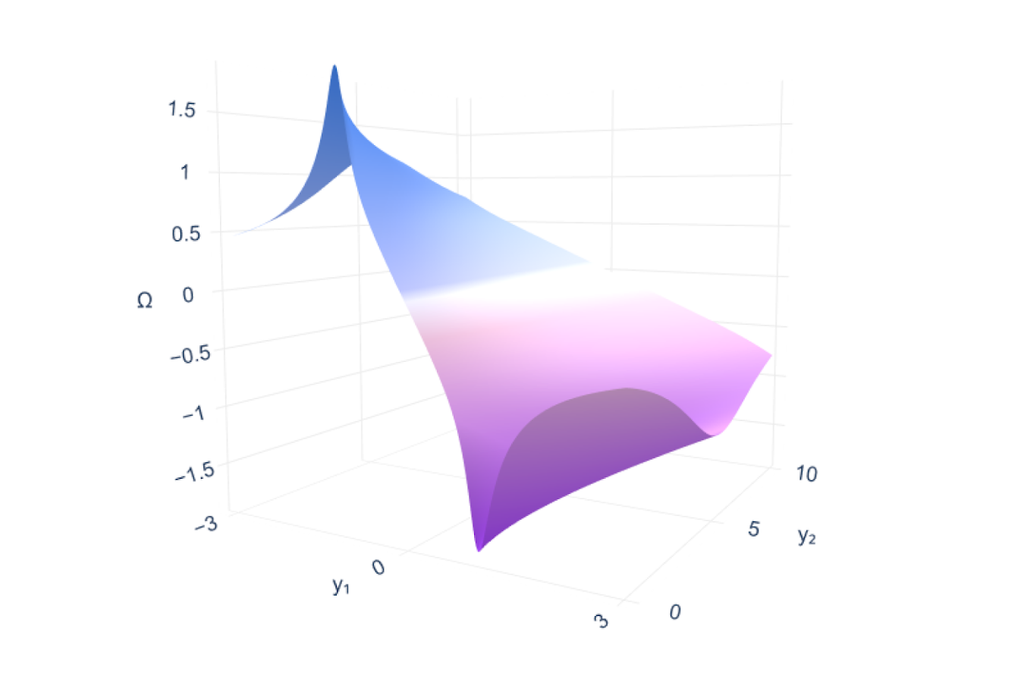
A descoberta dessas singularidades foi possível por causa de um avanço tecnológico onde eles conseguiram otimizar o treinamento. Essa otimização permitiu que o modelo fosse treinado com a precisão necessária para encontrar essas soluções. Segundo o autor, os maiores erros do modelo equivalem a prever o diâmetro da Terra com uma margem de apenas alguns centímetros.

A era da Física

As PINNs ajudam dentro do aprendizado de máquina porque não necessitam de grande volume de dados para aprenderem. Além disso, elas impedem que os sistemas que estão sendo aprendidos fujam da Física e encontrem soluções que não respeitam as leis de conservação. Essa abordagem acaba se tornando muito útil em problemas complexos, como o de Navier-Stokes, onde simulações convencionais exigem grande poder computacional ou apresentam limitações em cenários caóticos e não lineares.

Há alguns meses, diferentes especialistas na área e a tendência de artigos cada vez mais voltados para métodos com base na Física indicam que estamos entrando na era do Physical AI. No Physical AI, os modelos não apenas reconhecem padrões, mas também validam através de leis da Física. Ao unir IA e Física, torna-se possível resolver problemas de longa data em áreas como dinâmica de fluidos, materiais, clima e astrofísica.

Referência da notícia

Discovering new solutions to century-old problems in fluid dynamics